Overview
March 14, 3/14, or 3.14 is Pi Day. Those who live in countries that write the date backward may disagree and claim that Pi Day is 22 July (22 divided by 7). When I was young, I found the history of pi interesting, and I have never forgotten the anecdote of William Shanks.
A Brief History Of Pi
Pi, one of the most well-known mathematical constants (often represented by the lower-case Greek letter π), is the ratio of the circumference of a circle to its diameter. For any circle, the distance around the edge is slightly more than three times the distance across. Pi is an irrational number (a decimal number with no end and no repeating pattern). In fact, pi is the most widely studied number in all of mathematics. The number pi is essential to understanding geometry and has applications in physics, astronomy, mathematics, and space exploration. Used in architecture and construction, pi is an integral part of building everything from arches and bridges to the Pyramids of Giza.
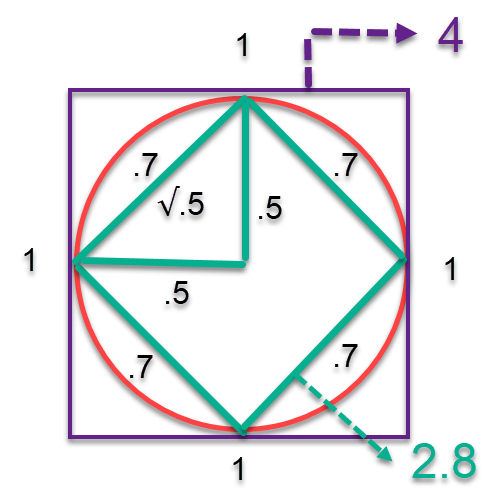
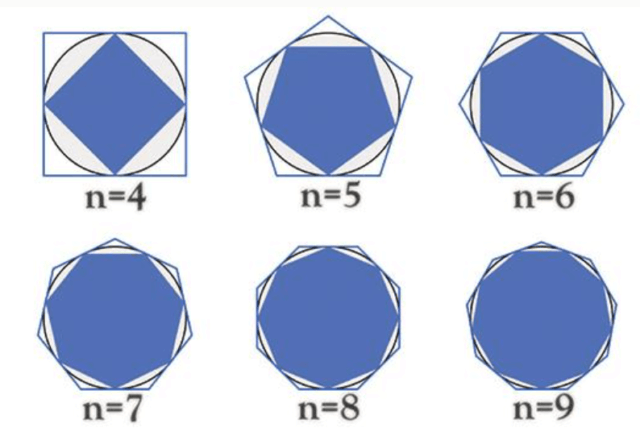
The ancients knew about pi, but since they had no method to calculate a curve, they approximated pi to 3. Around 250 BC, Archimedes, a Greek mathematician, was the first to use an algorithmic approach to calculate pi. Archimedes drew a polygon inside a circle, drew a second polygon outside of the circle, and calculated their perimeters. For example, the perimeters of four-sided polygons would result in pi being between 2.8 and 4. Archimedes continued adding more and more sides to both polygons, getting closer and closer to the shape of the circle. Stopping when he reached 96-sided polygons, Archimedes proved that pi is between 3.1408 and 3.1429. In other words, Archimedes calculated pi to two decimal places (almost three) with at least a 99.97% accuracy. For most real-world problems, this was more than enough.
Over the next two millennia, others continued to use Archimedes’ method to calculate pi. By 1610, Ludolph Van Ceulen had spent most of his 70-year life calculating pi to 35 decimal places. He used polygons with 4,611,686,018,427,387,904 sides! After his death, 3.14159265358979323846264338327950288 was engraved on his tombstone. In Germany, pi is still sometimes called the “Ludolphine number”.
In 1665-1666, Sir Isaac Newton was quarantined at home due to the Great Plague of London. During this time, Newton generalized the binomial theorem leading to his method of fluxions. What we now call calculus. After this, no one calculated pi using Archimedes’ method. What took Ludolph Van Ceulen decades to calculate could now be done in weeks.
William Shanks
Which brings us to William Shanks. Shanks spent many years using the Manchin formula to calculate pi to 530 decimal places. He published a book about it in 1853. In April 1873, twenty years later, Shanks published another book in which he expanded his calculation of pi to 707 decimal places. This calculation remained unchallenged until 1944 when D. F. Ferguson, working with a mechanical desk calculator, found that Shanks had mistakenly calculated the 528th digit. In other words, his calculation of pi was correct only for the first 527 digits. TWENTY YEARS DOWN THE DRAIN!
In 1949, John von Neumann was the first to use a computer (ENIAC-Electronic Numerical Integrator and Computer) to calculate pi. It took him 70 hours to calculate pi to 2,037 digits.
In 2022, Emma Haruka Iwao, taking approximately 158 days using Google Cloud, calculated pi to 100 trillion digits. This is the current world record.
My Pi History
After buying my first computer, I remembered the story of William Shanks and I wanted to see how fast I could calculate pi. I found a pi-calculation program, inserted the floppy drive, revved up the 8.0 MHz CPU, typed in the command lines, and watched as all 640 KB of memory came to life. After fifteen minutes, I had correctly calculated pi to 707 decimal places. TAKE THAT WILLIAM SHANKS! Later, I plugged in the program’s maximum capacity and calculated pi to about 35,000 decimal places in just 4 and ½ days!
Curious about how fast my current computer is, I looked for a modern pi-calculating program.
Calc Pi
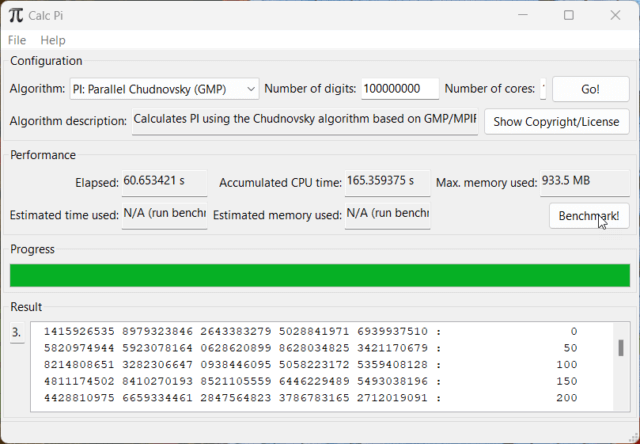
Calc Pi is a multi-platform program for calculating pi to arbitrary precision (the digits of precision are limited only by the available computer memory). Calc Pi also calculates Euler’s number (the base of the natural logarithm) also known as the mathematical constant e. Calc Pi has a simple GUI and can take advantage of multi-threaded CPUs. Calc Pi displays the result in the bottom half of the window when the calculation is complete. You can scroll down to see the calculated digits. The digits are grouped in tens, and 50 digits are displayed per line. The offset of the first digit is displayed on the right. To save the result to a file, use the menu item File -> Save Result.
My AMD Ryzen 7 5700U laptop with 16 GB of RAM can compute pi to 35,000 digits in 0.01 seconds and to 100 million digits in 61 seconds. William Shanks must be sobbing in his grave!
If you run the Calc Pi program, let me know in the comments how fast your computer is able to compute pi.
—

I have been in the sign business for thirty eight years. And have used the ‘golden ratio” Phi for many years. It helps me create better looking logos and signs.
Phi, like Pi, is a ratio defined by a geometric construction.
Hi Jeffrey,
I know that in photography, two composition techniques I’m familiar with are the golden rule and the rule of thirds. These basic math concepts are used in so many places.
Unfortunately my search engines do not show Calc Pi only just a few methods to do so.
Can you give a link to it please – thanks.
Hi Otto,
The link is already in the article. After the Calc Pi Header, the paragraph begins with the words “Calc Pi”, on most browsers, it will be colored blue. That is the link, if you hover your mouse over it, it should show the URL address somewhere on your browser. If you click on it, it will take you to the Calc Pi homepage. Then, look for the Calc Pi Download link on that page.
Oh, so it is! Being color blind and using Dark Mode the link did not jump out for me. Thank you for letting me know.
I have an old lenovo T540p, 2nd hand.
Intel Core i5 4200M1@2.50GHz Haswell 22nm
(if that’s interesting)
10m digits; Elapsed 40.601190s;
Acc. CPU time 68.843750s
Max Memory used 117.0 MB
Ok, had to try Calc Pi for fun. Besides just recently upgraded my hardware to i7-12700k with 32GB DDR4 RAM so was curious what it would show compared to your numbers.
35,000 = .006s
100,000,000 = 38.3s
600,000,000 = 308.5s (5.14m)
Tried 1,000,000,000 but the application shut down.
Intel i5-11400 with 32GB DDR4 Ram:
35,000
Time 0.0085
CPU 0.031
Memory 618.4 MB
100,000,000
Time 53.54
CPU 142.56
Memory 959.2 MB
600,000,000
Time 431.11
CPU 1272.95
Memory 5.2 GB
@1,000,000,000, the app shut down, just like Jon S. Now it won’t run!
Will try removing then reinstalling.
I’m quite computer savvy, but trying to perform and really understand benchmarking has never been my thing. I just look at everyone else’s numbers to evaluate. So I find it interesting to see the difference between your rig and mine. Tried 1,000,000,000 again. Same result. Maybe an i9-13700k or more memory could handle it?
Hi Jon,
I tried 600,000,000 on my machine. It took 491 seconds. At 1,000,000,000 I received the same result as you. I have 16 GB on my machine, you have 32 GB. Therefore, I’m guessing that you should have enough memory. Technically, Calc Pi is not a bench marking program. It is a program that uses arbitrary precision (the digits of precision are supposed to be limited by the available computer memory).
My guess is that there is a limitation somewhere in Windows or the underlying programming language that will not allow a calculation over a certain value.
Yes, I realize it is not a benchmarking tool, but it is interesting to see how faster processors do indeed make a difference in the speed of calculation. Compared to some of the stats in the original article, it’s quite amazing how fast today’s processors are.
Yeah, there may be a limit somewhere, where even a faster machine may not be able to do it.